CALCULATION OF THE POSITION OF THE CENTRE OF PRESSURE

The following example of how to calculate an arrow center of pressure makes two basic simplifications. Firstly the arrow is assumed not to be rotating (fishtailing). If the arrow is rotating then the air velocity (and hence the drag) varies along the arrow. Secondly the shape of the fletchings is assumed to be a right angled triangle, the nearest simple shape that approximates to a fletching.

The approach is first to calculate the total pressure and center of pressure locations for the shaft drag, fletching drag and Munk moment individually and then calculate the arrow total pressure and center of pressure location from the three components.

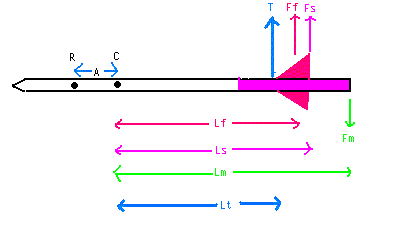
In the diagram the total drag force (T) acts at the arrow center of pressure at distance (Lt) behind the center of gravity (C). The total drag is the sum of the fletching drag (Ff), the shaft drag (Fs) and the Munk moment (Fm). The distances from the center of gravity to the fletching drag, shaft drag and Munk moment centers of pressure are Lf, Ls and Lm respectively. The resulting axis of rotation of the arrow (R) is at a distance 'A' in front of the arrow center of gravity.

If you equate the moments for the arrow total pressure/center of pressure to the individual shaft/fletchings/Munk moment total pressures/centers of pressure you end up with the distance Lt being given by:-

Lt = (Fs Ls + Ff Lf - Fm Lm)/(Fs+Ff-Fm)

Example

Suppose the arrow is 80 cm long and 0.5 cm diameter. The arrow FOC is 13%. The fletchings are assumed to be 2.5 cm long with each fletching having a total area of 3.5 square cm. The front of the fletchings are fitted 73 cm from the front of the shaft. There are 3 fletchings fitted at 120 degrees to the shaft and they are assumed to be triangular in shape.

To make life simple it is assumed that the drag properties of the shaft and fletchings are identical so instead of drag forces we can use drag areas. (main difference is in the shaft and fletching drag coefficients).

With an FOC of 13% the center of gravity is 10.4 cm in front of the center of the shaft.

Munk Moment

The value of Fm is assumed at 1.5 square cms. (based on some rough measurements made some years ago).The center of pressure is assumed to act at the back of the arrow so Lm = 80/2 + 10.4 = 54 cms.

Shaft Drag

The shaft area contributing to rotational drag Fs = 2 x 10.4 x 0.5 = 10.4 square cms. (see section on FOC). Because of symmetry the distance Ls is half the shaft length i.e. 40 cms

fletching

For a triangular fletching the centre of pressure horizontal position is 2/3 distance along the base from the front. (The vertical position doesn't matter as the fletchings are assumed not to be spinning the arrow)

i.e. Lf = 73 + 2.5 x 2 / 3 - (40-10.4) = 45.07 cms

The effective area Ff of the fletchings = 1.5 x 3.5 = 5.25 square cms.

(the multiplier 1.5 allows for the fletching angle = 2 x sin squared (alpha/2) where alpha is the angle between fletching).

Lt is therefore (10.4 x 40 + 5.25 x 45.07 - 1.5 x 54)/(10.4 + 5.25 - 1.5) = 40.4 cms

i.e. the center of pressure is 40.4 centimeters behind the arrow center of gravity.

Any arrow rotation will have the effect of moving the center of pressure further back so the 40.4 cms represents the minimum distance between the center of gravity and the center of pressure. (With e.g. fishtailing the influence of the shaft drag decreases and the influence of the fletching drag and Munk moment increases)

If 'Ig' is the arrow moment of inertia at the center of gravity and 'M' is the total arrow mass then the distance of the arrow axis of rotation in front of the center of gravity 'A' is given by:-

A = Ig / (Lt x M)

e.g. if Ig was 5400 gm cm squ. and M was 18 gms then A = 5400/(40.4 x 18) = 7.4 cms

Top Page

Return to main Index