When (p,q) = (5,2), the resulting shape is a five pointed star, or pentagram. A pentagram also results when all five diagonals of a regular pentagon are drawn.
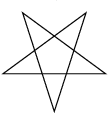
The pentagram, or five-pointed star
This document shows how one could draw a geometrically perfect pentagram,
using "Ancient Greek Style" (that is, using only a straight-edge and compass).
| A (p,q) Star Polygon is defined in the
following way: Take a circle with p evenly spaced points along its circumference. From
each of the p points, draw line segments from that point to every qth point
around the circle. The segments make up the Star Polygon. When (p,q) = (5,2), the resulting shape is a five pointed star, or pentagram. A pentagram also results when all five diagonals of a regular pentagon are drawn. |
|
Let X be the desired length of one of the
five long segments that will make up the pentagram. Construct rectangle ABCD, where
segment AB = X and BC = X / 2. 1
Draw the diagonal AC.
| A | 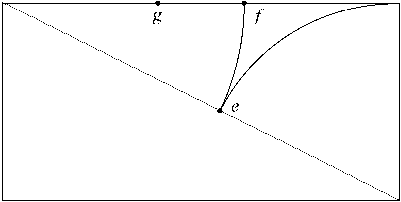 |
B |
| D | C |
Find point e on the diagonal such that Ce = BC. This can be done by putting the compass point at C, its stylus at B, and drawing the arc from B until it meets the diagonal AC (this point on the diagnoal will be called e). Let f be the point on the top side of the rectangle, such that Af = Ae. f can be found in a way similar to how point e was found: using the compass to draw arc ef.
Point f creates a golden cut for segment AB. Point g is a second golden cut which can be found by the same procedure.2 Just apply the same steps to the left half of the rectangle.
The only item now needed from the diagram is segment Agfb; the rest can be erased.
| A | g |
f |
B |
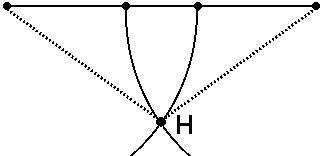
With the compass point at A, and stylus on f draw an arc below the line. Similarly, let the compass touch points B and g and draw an arc on the right-hand side side. The arcs will intersect at point H (which should fall along AB's bisector, if it were drawn).
| A | g |
f |
B | |
 |
||||
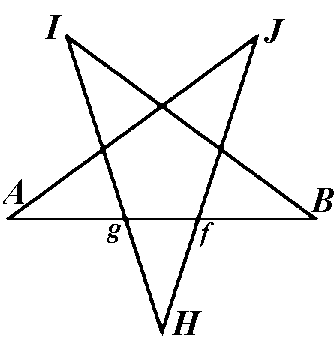
Now it's only a matter of "connect the dots". Draw a line from H to g, extending it to a length equal to that of AB. Likewise, draw a line from H through f, extending it to the same length as AB. Mark these end points as I and J. Connect A to J, and B to I. Erase any extraneous pencil marks. The result is a mathematically precise pentagram.3
In some religious and aesthetic traditions, a circle is used to incribe the pentagram. If one wanted to draw a circle around the star, follow this procedure:
Use the straight-edge to draw two lines, one connecting g to J, the other connecting f to I. The intersection of these lines will mark the center of the pentagram and thus the center of the desired circle. Place the point of the compass at this center point, and the stylus at any of the outter five points (say, point I). With the radius and the center now known, simply draw the entire circle with the compass.
While this process will create a perfect pentagram in theory, it might not be absoultely perfect in practice. As with any procedure involving measurement, there will be slight errors in drawing lines, compasses usually leave holes in paper, etc. Still, the results will typically yield much better results than a purely "freehand" attempt.
1 - I've omitted the details, but rectangle
ABCD can be drawn using only a straight edge and compass, since for a given segment it's
possible to find any of the following: a segment half its length, a parellel segment, and
a perpendicular segment. One could first define length X with the compass (which is the
only allowed way to measure lengths), draw segment AB of that length, and find the
perpendicular bisector of . From there, length X/2 can be easily found. After finding
another line perpendicular to AB, and thus being able to find two perpendiculars X/2 in
length, it's easy to draw a line parellel to AB and X/2 units away. A little playing with
the geometry will eventually yield the desired rectangle ABCD
2 - It would seem that since aF will be of the same length as Bg, that one could just
measure Bg to find g after already having the compass length set to that of aF. But this
would break one of the "rules" the Greeks had: when you pick the compass off of
the paper, the span of the compass is considered to be reset!
3 - The pentagram contains many golen triangles and golden cuts, and some work with the
geometry will show that these lines do, in fact, produce a precise pentagram. To see why f
(and thus g) is a golden cut: first note that triangle Afh is a golden triangle (the three
angles are 36, 36, and 72 degrees). Triangle JBf is congruent to Afh. This means the ratio
of length Af to fb is the golden mean (1.618...), and thus f is a golden cut for AB.
Top Page
Return to main Index